Bloque II
Bloque II
FUNCIÓNES POLINOMIALES
Modelo algebraico general de funciones polinomiales
Función lineal
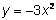
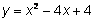
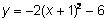
Formas, estándar y factorizada
Funciones polinómicas de grado 0:
Funciones polinómicas de primer grado:
.
video:
https://www.youtube.com/results?search_query=teorema+de+residuo
video:
https://www.youtube.com/watch?v=l6N9pj4s5QM
FUNCIÓNES POLINOMIALES
Modelo algebraico general de funciones polinomiales
Función lineal
la noción de función tiene diversos usos. En esta ocasión, nos vamos a centrar en la función matemática: la relación que se establece entre dos conjuntos, a través de la cual a cada elemento del primer conjunto se le asigna solo un elemento del segundo conjunto, o ninguno.
Con esto en claro, podemos avanzar en la idea de función lineal. Así se denomina a la función matemática compuesta por variables de primer grado. Cabe destacar que una variable es una magnitud que, en el marco de un cierto conjunto, puede adoptar cualquiera de los valores posibles.
Las funciones lineales se representan con una línea recta en el plano cartesiano. Es importante tener en cuenta que lo que hacen las funciones, en definitiva, es expresar una relación entre variables, pudiéndose desarrollar modelos matemáticos que representen este vínculo.
Modelo grafico- La ordenada al origen "b" es el valor donde la recta corta al eje “y”
- El valor de la pendiente determina que una función afín sea creciente, constante o decreciente.
Ejemplo: y = 2x ► m = 2 y b = 0
¿Cómo se hace la gráfica de la función afín a partir de la formula?
Forma Práctica: hay que seguir los siguiente pasos
1ro: se ubica en el eje de ordenadas “y” la ordenada al origen “b”.
2do: a partir de ese punto nos corremos una unidad a la derecha (siempre).
3ro: a partir de allí si la pendiente es (+) subimos las unidades que indica la pendiente y si es (-) bajamos la cantidad de unidades que indica la pendiente
4to: Unimos los dos puntos, el de la ordenada al origen(sobre el eje "y" y el punto a donde nos llevo la pendiente
Ejemplo: y = 3x – 2 ► m = 3 y b = - 2
1ro, ubicamos en el eje “y” la ordenada al origen b = - 2
2do Nos corremos una unidad a la derecha
3ro, subimos 3 unidades porque la pendientees positiva (+)
4to, unimos los dos puntos, el de la ordenada
al origen y el punto al que nos llevo la pendiente
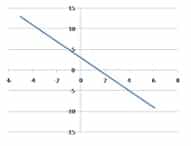
Ejemplo: y = - 2x + 4 ► m = - 2 y b = 4
1ro, ubicamos en el eje “y” la ordenada al origen b = 4
2do Nos corremos una unidad a la derecha
3ro, como la pendiente es (-) bajamos 2 unidades
4to, unimos los dos puntos, el de la ordenada al origen y el punto al que nos llevo la pendiente
Funciones cuadráticas
Una función cuadrática es una función que puede ser descrita por una ecuación de la forma y = ax2 + bx + c, donde a ≠ 0. Ningún término en la función polinomial tiene un grado mayor que 2. Las funciones cuadráticas son útiles cuando trabajamos con áreas, y frecuentemente aparecen en problemas de movimiento que implican gravedad o aceleración.
Las gráficas de las funciones cuadráticas tienen características que están estrechamente relacionadas con su forma simbólica. A medida que exploremos estas gráficas, aprenderemos a identificar estas características, y veremos algunas de las maneras de estructurar las ecuaciones cuadráticas.
Una función cuadrática es un polinomio de grado 2, es decir, el exponente más alto en la variable es 2. Los siguientes son ejemplos de funciones cuadráticas:
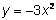
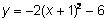
La función cuadrática más básica y simple tiene la ecuación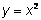 
. Si hacemos una tabla con los valores de esta función, vemos que el rango (los valores de y, o salida) no se comportan como una función lineal. En una función lineal, el valor de y cambia por la misma cantidad cada vez que el valor de xaumenta por 1. Eso no sucede con una función cuadrática:
. Si hacemos una tabla con los valores de esta función, vemos que el rango (los valores de y, o salida) no se comportan como una función lineal. En una función lineal, el valor de y cambia por la misma cantidad cada vez que el valor de xaumenta por 1. Eso no sucede con una función cuadrática:
x
|
y = x2
|
-3
|
9
|
-2
|
4
|
-1
|
1
|
0
|
0
|
1
|
1
|
2
|
4
|
3
|
9
|
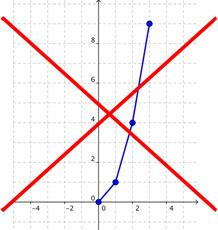
Los valores de y no cambian por una cantidad constante. Grafiquemos algunos puntos para ver cómo se vería la función:
Después de graficar algunos puntos, podría ser tentador conectar los puntos con segmentos de línea, que son rectos. Pero esto estaría mal, y produciría un patrón que no representa la función.
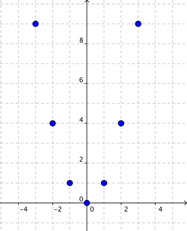
Borremos esas líneas rectas y grafiquemos el resto de los puntos:
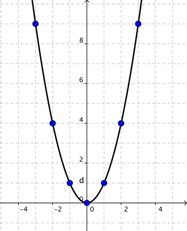
Ahora dibujamos una curva suave conectando los puntos.
¡Mejor! Una función cuadrática resulta en una gráfica con forma de U, llamada parábola. Los valores de la función cambian suavemente, por lo que la curva debe ser suave también. Ahora que podemos ver la naturaleza de la parábola (forma de U), veamos su forma en detalle.
Formas, estándar y factorizada
La forma estándar de una ecuación cuadrática es y = ax^2 + bx + c, donde a, b y c son coeficientes y la y y la x son variables. Es más fácil resolver una ecuación cuadrática cuando está en su forma estándar ya que puedes computar la solución con a, b y c. De todos modos, si necesitas graficar la función cuadrática, o parábola, el proceso es más simple cuando la ecuación está en la forma canónica. Esta es de la forma: y = m(x-h)^2 + k.
Pasos para convertir una función cuadrática en su forma general a estándar:
- Factoriza el coeficiente a de los dos primeros términos de la ecuación de forma estándar y colócalos afuera de los paréntesis. Por ejemplo, si estás convirtiendo 2x^2 - 28x + 10 a la forma canónica, primero escribe 2(x^2 - 14x) + 10.
- Divide el coeficiente del término x dentro del paréntesis por dos, luego tómale la raíz cuadrada. En el ejemplo, el coeficiente x dentro de los paréntesis es -14. Computa -14/2 que es igual a -7, y luego (-7)^2 que es igual a 49.
- Agrega el número dentro del paréntesis, y luego balancea la ecuación, multiplícala por el factor afuera del paréntesis y resta este número de la ecuación cuadrática completa. Por ejemplo, 2(x^2 - 14x) + 10 se vuelve 2(x^2 - 14x + 49) + 10 - 98, ya que 49*2 = 98.
- Simplifica la ecuación combinando los términos en el extremo final. Por ejemplo 2(x^2 - 14x + 49) - 88, ya que 10 - 98 = -88.
- Convierte los términos dentro de los paréntesis a una unidad cuadrada de la forma (x - h)^2. El valor de h es la mitad del coeficiente del término x. Por ejemplo, 2(x^2 - 14x + 49) - 88 se transforma en 2(x - 7)^2 - 88. La ecuación cuadrática ahora está en su forma canónica.
Funciones de grado superior
Una función polinómica es aquella que está definida por un polinomio:
donde a0, a1 ... an-1, an son números reales que se llaman coeficientes del polinomio y n es el grado del polinomio.
Las características generales de las funciones polinómicas son las siguientes:
1) El dominio de definición es el conjunto de los números reales (R).
2) Son siempre continuas.
3) No tienen asíntotas.
4) Cortan al eje X, como máximo, un número de veces igual que el grado del polinomio.
5) Cortan el eje Y en el punto (0, a0).
6) El número de máximos y mínimos relativos es, a lo sumo, igual al grado del polinomio menos uno.
7) El número de puntos de inflexión es, a lo sumo, igual al grado del polinomio menos dos.
Funciones polinómicas de grado 0:
rectas horizontales
Funciones polinómicas de primer grado:
rectas oblicuas
Funciones polinómicas de segundo grado: parábolas
Funciones polinómicas de tercer grado: cúbicas
Funciones polinómicas de cuarto grado: cuárticas
El Teorema del residuo
Generalmente cuando un polinomio es dividido entre un binomio hay un residuo.
Considere la función polinomial f ( x ) = x 2 - 8x + 6. Divida el polinomio entre el binomio x - 2.
Podemos realizar la división en cualquier método.
Método 1: División larga
.
El residuo es -6.
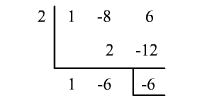
Método 2: División sintética
El residuo es -6.
Ahora compare el residuo de -6 en f (2).
Dese cuenta que el valor de f (2) es el mismo que el residuo cuando el polinomio es dividido entre el binomio x - 2. Esto ilustra el teorema del residuo.
Si un polinomio f ( x ) es dividido entre x - a , el residuo es la constante f ( a ), y
, donde q ( x ) es un polinomio con un grado menor que el grado de f ( x ).
, donde q ( x ) es un polinomio con un grado menor que el grado de f ( x ).
En otras palabras, el dividendo es igual al cociente por el divisor mas el residuo.
La división sintética es un proceso más sencillo para dividir un polinomio entre un binomio. Cuando es utilizada la división sintética para evaluar una función, es llamada la sustitución sintética.
video:
https://www.youtube.com/results?search_query=teorema+de+residuo
Teorema del factor
Si a es una raiz de ƒ(x), entonces x - a es un factor del polinomio, donde a es un número real.
Aqui podemos observar la importancia de conocer el valor del residuo, ya que si éste es igual a cero, nos va a indicar que hemos encontrado un factor del polinomio y con él, una raiz del polinomio (una solución a la ecuación polinomial ƒ(x) = 0).
Si a es una raiz de ƒ(x), entonces x - a es un factor del polinomio, donde a es un número real.
Aqui podemos observar la importancia de conocer el valor del residuo, ya que si éste es igual a cero, nos va a indicar que hemos encontrado un factor del polinomio y con él, una raiz del polinomio (una solución a la ecuación polinomial ƒ(x) = 0).
Ejercicio
Comprueba que los siguientes polinomios tienen como factores los que se indican:
1.-(x3 − 5x − 1) tiene por factor (x − 3)
(x3 − 5x −1) es divisible por (x − 3) si y sólo si P(x = 3) = 0.
P(3) = 33 − 5 · 3 − 1 = 27 − 15 − 1 ≠ 0
(x − 3) no es un factor.
2.-(x6 − 1) tiene por factor (x + 1)
(x6 − 1) es divisible por (x + 1) si y sólo si P(x = − 1) = 0.
P(−1) = (−1)6 − 1 = 0
(x + 1) es un factor.
3.-(x4 − 2x3 + x2 + x − 1) tiene por factor (x − 1)
(x4 − 2x3 + x2 + x − 1) es divisible por (x − 1 ) si y sólo si P(x = 1) = 0.
P(1) = 14 − 2 · 13 + 1 2 + 1 − 1 = 1 − 2 + 1 + 1 − 1 = 0
(x − 1) es un factor.
Tratamiento visual de máximos y mínimos
Los máximos y mínimos de una funciónson los valores más grandes o más pequeños de ésta, ya sea en una región o en todo el dominio.
Los máximos y mínimos en una función fson los valores más grandes (máximos) o más pequeños (mínimos) que toma la función, ya sea en una región (extremos relativos) o en todo su dominio (extremos absolutos).
Los máximos y mínimos también se llaman extremos de la función
Máximos y mínimos absolutos
Los extremos absolutos también reciben el nombre de extremos globales.
https://www.youtube.com/watch?v=l6N9pj4s5QM
Máximos y mínimos relativos
Los extremos relativos de una función fson los valores más grandes (máximos) o más pequeños (mínimos) de una región del dominio.
Los extremos relativos también son conocidos como extremos locales.
- La función f tiene en M un máximo relativo si f(M) es mayor que sus valores próximos a izquierda y derecha.En términos de sus derivadas, sean f y f ’ derivables en M. Entonces M es máximo relativo de f si:
También se puede decir que M es un máximo relativo en su entorno si a la izquierda la función es creciente y a la derecha decreciente. - La función f tiene en m un mínimo relativo si f(m) es menor que sus valores próximos a izquierda y derecha.En términos de sus derivadas, sean f y f ’ derivables en m. Entonces m es mínimo relativo de f si:
También se puede decir que m es un mínimo relativo en su entorno si a la izquierda la función es decreciente y a la derecha creciente
Comentarios
Publicar un comentario