Bloque IV

Bloque VI
Funciones trascendentes

 Función exponencial

En matemáticas, una función exponencial es una función de la forma.en el que el argumento x se presenta como un exponente. Una función de la forma  también es una función exponencial, ya que puede reescribirse como
Funciones exponenciales
Exponentials.svg
video:

Función algorítmica
En estas funciones, a es la base, que tiene que ser positiva y diferente de 1. La forma oficial de leer esta ecuación es la siguiente: «la función de x es igual al logaritmo base a de x». Cabe mencionar que también podría expresarse sin el uso de la expresión f(x), sino con una variable tal como y, ya que de este modo podríamos reflejar con mayor claridad que el resultado es un elemento diferente, de otro conjunto.
Es importante mencionar que la función logarítmica es la función inversa de la función exponencial: aquella que se representa con la ecuación f(x) = aˣ
Entre las principales características de una función logarítmica, podemos mencionar que su dominio (su conjunto de partida o inicial) son los números reales positivos. Se trata de una función continua, cuyo recorrido es R (las imágenes que se obtienen de aplicar la función corresponden a cualquiera de los elementos del conjunto formado por los números reales).
En el ambito de las matemáticas, se conoce con el nombre de función inyectivaa aquélla en la cual a cada elemento del codominio le corresponde solamente uno del dominio. Dicho en otras palabras, en una función de este tipo, al que también pertenece la logarítmica, no se puede dar el caso de que más de un elemento del primer conjunto tenga la misma imagen.
  1. El dominio es el conjunto de todos los números reales positivos.
  2. El rango es el conjunto de todos los números reales.
    (Ya que la función logarítmica es la inversa de la función exponencial, el dominio de la función logarítmica es el rango de la función exponencial y el rango de la función logarítmica es el dominio de la función exponencial)
  3. La función es continua y uno-a-uno.
  4. El eje de las y es la asíntota de la gráfica.
  5. La gráfica intersecta al eje de las x en (1, 0). Esto es, la intercepción en x es 1.
La función logarítmica, y = log b x , puede ser cambiada en k unidades verticalmente y hunidades horizontalmente con la ecuación y= log b ( x + h ) + k .
Cambio Vertical
Si k > 0, la gráfica se desplazaría k unidades hacia arriba.
Si k < 0, la gráfica se desplazaría k unidades hacia abajo.
Cambio Horizontal
Si h > 0, la gráfica se desplazaría h unidades a la izquierda.
Si h < 0, la gráfica se desplazaría h unidades a la derecha.

video:

https://www.youtube.com/watch?v=EDCXR0WUC5k

Función logarítmica natural

El logaritmo con base e es llamado el logaritmo natural. Se denota por ln x . La función logarítmica natural, y = ln x es la inversa de la función exponencial natural de base, y = e x .
La gráfica de la función logarítmica natural y= ln x se muestra a continuación.
Ejemplo:
Grafique la función y = log 10 ( x – 1) + 2.
Comience con la gráfica logarítmica básicay = log b x . Luego cambie la gráfica 1 unidad a la derecha y 2 unidades hacia arriba.


Funciones exponenciales y algorítmicas
Funciones trigonométricas
La función seno
Definición geométrica
El seno de un número real t es la coordenada y(altura) del punto P en el siguiente diagrama, donde |t| es el largo del arco que se indica.

sin t = coordenada y del punto P
Definición "rueda bicicleta"
Si una rueda cuyo radio es 1 roda hacia delante a una velocidad de 1 unidad por segundo, sin t el la altura de un marcador fijo en su neumático después de t segundas, si se empieza a medio camino entre la parte superior y la parte inferior de la rueda.
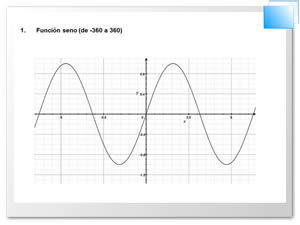
Gráfica de la función seno 

y = sin x
Función seno general 
La función seno "generalizado" tiene la siguiente forma:

y = A sin[ω(x - α)] + C
  • A es la amplitud (la altura de cada máximo arriba de la línea base).
  • C es el desplazamiento vertical (la altura le la línea base).
  • P es el periodo o longitud de onda (el longitud de casa ciclo).
  • ω es la frecuencia angular, y se expresa por 
            ω= 2π/P o P = 2π/ω.
  • α es el desplazamiento de faso.
Ejemplos
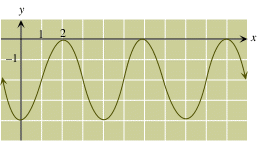
Considere la siguiente gráfica, que muestra una curva de seno "general" (desplazada y escalada):
Pregunta ¿Que es la ecuación de la gráfica?
Contesta Consultando la función seno generalizado a la izquierda, vemos que la ecuación de esta curva es:
    y = A sin[ω(x-α)] + C,
donde
  • La línea base (el punto medio de oscilación) se ubica 2 unidades abajo del eje x
  • A = amplitud (la altura de cada máximo arriba de la línea base) = 2
  • C = desplazamiento vertical = coordenada y de la línea base = -2
  • P = periodo (el longitud de casa ciclo, o distancia de un máximo al siguiente) = 4
  • ω = frecuencia angular = 2π/P = 2π/4 = π/2
  • α = desplazamiento de faso = 1 Esta es la distancia horizontal del eje y al primero punto donde la gráfica cruza la línea base.
Entonces, la ecuación de la curva más arriba es
    y = 2 sin[π/2 (x - 1)] - 2
Para comprobar que sirve esta ecuación, pruebela en la evaluador y graficador de funciones o en la graficador Excel (si tienes Excel en su computadora).

video:
https://www.youtube.com/watch?v=ATcTctC1Ei4
La función coseno
Definición geométrica
El coseno de un número real t es la coordenada x del punto P en el siguiente diagrama, donde |t| es el largo del arco que se indica.

cos t = coordenada x del punto P
sin t = coordenada y del punto P
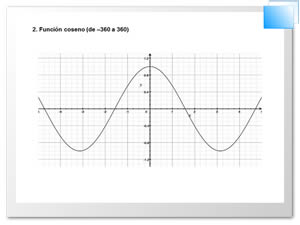
Gráfica de la función coseno 

y = cos x
Función coseno general
La función coseno "generalizado" tiene la siguiente forma:

y = A cos[ω(x - α)] + C
  • A es la amplitud (la altura de cada máximo arriba de la línea base).
  • C es el desplazamiento vertical (la altura le la línea base).
  • P es el periodo o longitud de onda (el longitud de casa ciclo).
  • ω es la frecuencia angular, y se expresa por 
            ω= 2π/P o P = 2π/ω.
  • α es el desplazamiento de faso.
Ejemplos
Considere la siguiente gráfica, que muestra la misma curva de seno "general" (desplazada y escalada) que más arriba:
Pregunta ¿Esta vez, que es su ecuación, esta vez escrita como una función coseno general?
Contesta Consultando la función coseno generalizado a la izquierda, vemos que la ecuación de esta curva es:
    y = A cos[ω(x-α)] + C,
donde
  • La línea base (el punto medio de oscilación) se ubica 2 unidades abajo del eje x
  • A = amplitud (la altura de cada máximo arriba de la línea base) = 2
  • C = desplazamiento vertical = coordenada y de la línea base = -2
  • P = periodo (el longitud de casa ciclo, o distancia de un máximo al siguiente) = 4
  • ω = frecuencia angular = 2π/P = 2π/4 = π/2
  • α = desplazamiento de faso = 2 Es distinto para coseno: la distancia horizontal del eje y al primero máximo.
Entonces, la ecuación de la curva más arriba es:
    y = 2 cos[π/2 (x - 2)] - 2
Para comprobar que sirve esta ecuación, pruebela en la evaluador y graficador de funciones o en la graficador Excel (si tienes Excel en su computadora). 

video:
https://www.youtube.com/watch?v=Dgpsd_CwZfs
Identidades trigonométricas fundamentales: Relaciones entre seno y coseno
El seno y coseno de un número t se relacionan con
    sin2t + cos2t = 1
Podemos obtener la curva coseno desplazando la curva seno hacia la izquierda una distancia igual a π/2. A la inversa, podemos obtener la curva seno desplazando la curva coseno π/2 hacia la derecha. Estos hechos se puede expresar como sigue
    cos t = sin(t + π/2) 
    sin t = cos(t - π/2)

Gráficas de las funciones trigonométricas

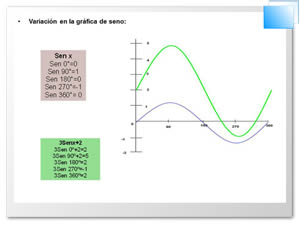
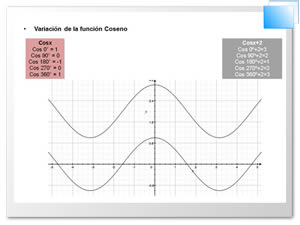
Si queremos representar en forma gráfica una función trigonométrica tomamos los valores de la variable independiente como abscisas y los valores de la función como ordenadas, obteniendo así una serie de puntos, los que al unirlos nos dará una línea que será la representación gráfica de la función.
Uso de la función seno: ésta se usa cuando en un triángulo rectángulo se conoce un ángulo agudo y el cateto opuesto, o un ángulo agudo y la hipotenusa, o el cateto  opuesto al ángulo dado.
Uso de la función coseno: si en un triángulo rectángulo conocemos un ángulo agudo y el cateto adyacente, o un ángulo agudo y la hipotenusa.
Podemos calcular el cateto adyacente al ángulo dado y la hipotenusa usando esta función.
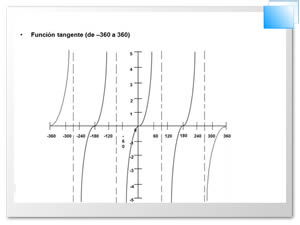
Uso de la función tangente: si en un triángulo rectángulo conocemos un cateto y el ángulo adyacente a él podemos calcular el otro cateto.
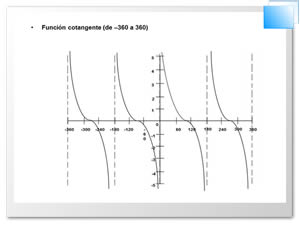
Uso de la función cotangente: por lo tanto en todo triángulo rectángulo si conocemos un cateto y su ángulo opuesto podemos calcular el valor del otro mediante ésta.
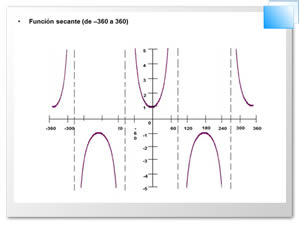
Uso de la función secante: ésta se usa cuando se tiene lo contrario que en la función coseno.
Uso de la función cosecante: ésta se usa cuando se tiene lo contrario a la función seno.























Comentarios

Publicar un comentario

Entradas más populares de este blog

DOMINIO, CODOMINIO Y RANGO

Imagen
                                                                                            En su forma más simple el dominio son todos los valores a los que aplicar una función, y el rango son los valores que resultan. Dominio: Se llama dominio de definición de una función f, y se designa por Dom f, al conjunto de valores de x para los cuales existe la función, es decir, para los cuales podemos calcular y = f(x). Se dice que el dominio de una función son todos los valores que puede tomar el conjunto del dominio y que encuentra correspondencia en el conjunto llamado codominio. El dominio es el intervalo de valores que están sobre el eje de las X y que nos generan una asociación en el eje de las Y . Codominio y rango:  El codominio y el rango tienen que ver con la salida, pero no son exactamente lo mismo. El codominio es el conjunto de valores que podrían salir. El rango es el conjunto de valores que realmente salen. Ejemplo:   puedes definir una función
Leer más

Bloque II

Imagen
Bloque II FUNCIÓNES POLINOMIALES   Modelo algebraico general de funciones polinomiales Función lineal la noción de  función  tiene diversos usos. En esta ocasión, nos vamos a centrar en la  función matemática : la  relación  que se establece entre dos conjuntos, a través de la cual a cada elemento del primer conjunto se le asigna solo un elemento del segundo conjunto, o ninguno. Con esto en claro, podemos avanzar en la idea de  función lineal . Así se denomina a la  función matemática  compuesta por  variables de primer grado . Cabe destacar que una variable es una magnitud que, en el marco de un cierto conjunto, puede adoptar cualquiera de los valores posibles. Las funciones lineales se representan con una  línea recta  en el  plano cartesiano . Es importante tener en cuenta que lo que hacen las funciones, en definitiva, es expresar una  relación entre variables , pudiéndose desarrollar modelos matemáticos que representen este vínculo. Modelo grafico La ordenada al ori
Leer más